Python - ディープラーニング - 損失関数
公開日:2019-09-15
更新日:2019-09-15
更新日:2019-09-15
1. 概要
予測と正解がどれだけ一致しているかを評価するための損失関数についてです。
現在の重みが適切かどうかの判定に使います。
現在の重みが適切かどうかの判定に使います。
2. 動画
3. 損失関数
損失関数とは、現在のモデル(重み、バイアス、ニューラルネットワーク)によって出力される結果と、正解の誤差を算出する関数です。
この誤差が少なければ少ないほど、モデルの性能が良いと言うことになります。
損失関数はいくつかあり、目的によって使い分ける必要があります。
この誤差が少なければ少ないほど、モデルの性能が良いと言うことになります。
損失関数はいくつかあり、目的によって使い分ける必要があります。
3.1 二乗和誤差
回帰問題の損失関数としてよく使われます。
学習データ毎に「予測 - 正解」をして、結果を2乗した合計になります。
学習データ毎に「予測 - 正解」をして、結果を2乗した合計になります。
$$ E = \frac{1}{2}\sum_{k=1}^{n}{(y_k-t_k)^2} $$
n は学習データ数、y は予測結果(モデルの出力)、t は正解です。3.2 損失関数 - クロスエントロピー誤差(交差エントロピー誤差)
分類問題の損失関数としてよく使われます。
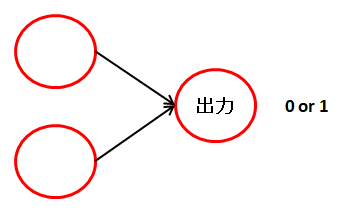
2値分類用。分類が2種類で、出力ノードが1つの場合に使います。
n は学習データ数、y は予測結果(モデルの出力)、t は正解(分類)です。
二値分類用の t には 0 か 1 が入り、この値自身が分類を意味します。one-hot表現ではないことに注意してください。
式には log が 2つありますが、log の前にある t と (1 - t) により、片方は常に 0 になります。
前半は分類(t)が 1 の場合の損失、後半は分類(t)が 0 の場合の損失を意味します。
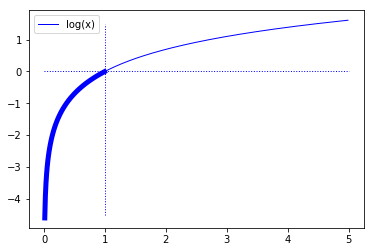
log は 0 ~ 1 の範囲では、1 に近いほど 0 に近くなり、0 に近いほど大きなマイナス値になります。

(例)学習データ1つあたりの損失
ニューラルネットワークの出力は1つだけになります。
また、log の 0 ~ 1 で損失を算出するため、出力の活性化関数も 0 ~ 1 の範囲に収めるシグモイド関数などを使う必要があります。

多値分類用。分類が2種類以上ある場合に使います。分類の数だけ出力ノードが必要になります。
n は学習データ数、y は予測結果(モデルの出力)、t は正解(分類)、m は分類数です。
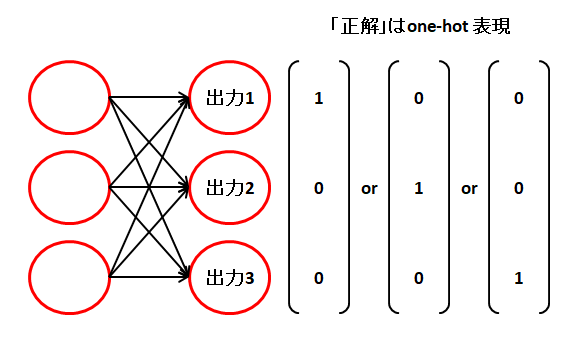
また、t は要素内に1つだけ 1 がある one-hot表現と呼ばれるベクトル(配列)にする必要があります。
(例) one-hot表現。1つだけ 1 があり、他は 0 になる。
(0 1 0 0)、(0 0 0 1)、(0 0 0 0 0 1 0 0)、(0 0 0 1 0 0 0 0)
外側のシグマは、全学習データの損失の平均を出すためのものです。2値分類のシグマと同じ。
内側のシグマは、出力ノード毎の損失(log)の合計を意味しますが、 実際には log の前の \( t_{ij} \) により、正解以外のノードは全て 0 になるため、正解の出力ノードだけの損失を意味します。
ニューラルネットワークは以下のようになり、分類の数だけ出力ノードが必要になります。
また、出力の活性化関数には、各出力が 0 ~ 1 の範囲になるソフトマックス関数などを使います。

2値分類用。分類が2種類で、出力ノードが1つの場合に使います。
$$ E = -\frac{1}{n}\sum_{i\,=\,1}^{n}{(t_i\,log\,y_i + (1-t_i)\,log(1-y_i))} $$
n は学習データ数、y は予測結果(モデルの出力)、t は正解(分類)です。
二値分類用の t には 0 か 1 が入り、この値自身が分類を意味します。one-hot表現ではないことに注意してください。
式には log が 2つありますが、log の前にある t と (1 - t) により、片方は常に 0 になります。
前半は分類(t)が 1 の場合の損失、後半は分類(t)が 0 の場合の損失を意味します。
log は 0 ~ 1 の範囲では、1 に近いほど 0 に近くなり、0 に近いほど大きなマイナス値になります。
(例)学習データ1つあたりの損失
| 予測 \( y_i \) | 正解 \( t_i \) | 損失 \( t_i\,log\,(y_i) \) | 損失 \( (1-t_i)\,log\,(1 - y_i) \) |
|---|---|---|---|
| 0.2 | 0 | 0 | -0.22 |
| 0.8 | 0 | 0 | -1.61 |
| 0.2 | 1 | -1.61 | 0 |
| 0.8 | 1 | -0.22 | 0 |
ニューラルネットワークの出力は1つだけになります。
また、log の 0 ~ 1 で損失を算出するため、出力の活性化関数も 0 ~ 1 の範囲に収めるシグモイド関数などを使う必要があります。
多値分類用。分類が2種類以上ある場合に使います。分類の数だけ出力ノードが必要になります。
$$ E = -\frac{1}{n}\sum_{i\,=\,1}^{n}{\sum_{j\,=\,1}^{m}{(t_{ij}\,log\,y_{ij})}} $$
n は学習データ数、y は予測結果(モデルの出力)、t は正解(分類)、m は分類数です。
また、t は要素内に1つだけ 1 がある one-hot表現と呼ばれるベクトル(配列)にする必要があります。
(例) one-hot表現。1つだけ 1 があり、他は 0 になる。
(0 1 0 0)、(0 0 0 1)、(0 0 0 0 0 1 0 0)、(0 0 0 1 0 0 0 0)
外側のシグマは、全学習データの損失の平均を出すためのものです。2値分類のシグマと同じ。
内側のシグマは、出力ノード毎の損失(log)の合計を意味しますが、 実際には log の前の \( t_{ij} \) により、正解以外のノードは全て 0 になるため、正解の出力ノードだけの損失を意味します。
ニューラルネットワークは以下のようになり、分類の数だけ出力ノードが必要になります。
また、出力の活性化関数には、各出力が 0 ~ 1 の範囲になるソフトマックス関数などを使います。