Python - ディープラーニング - 勾配降下法

公開日：2019-09-25 更新日：2019-09-25
[Python]

1. 概要

損失関数を使うとモデルを評価できますが、損失が最小となる重みを知ることができません。
損失をグラフにすると、すぐに最小値がわかりますが、実際に行おうとすると、全ての範囲で損失を求める必要があり、時間がかかります。
そこで勾配降下法を使用すると、少ない回数の計算で、最小値を求めることができます。
（参考：微分で最小値を求める方法）

勾配降下法は、以下の流れで最小値を求めます。
1. 関数を微分して傾きを調べる
2. 傾きが下がっている方に変数の値を徐々に移動させる
3. 傾きがほぼ水平になるところまで上記を繰り返す


2. 動画



3. 勾配降下法の実装

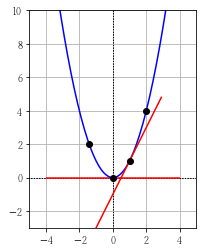
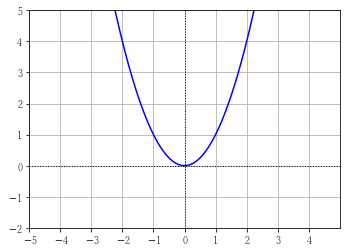
\( y = x ^ 2 \) の最小値を勾配降下法を使用して求めてみます。


3.1 微分

計算式がわかっているため、事前に微分しておきます。
事前に微分できない場合は、数値微分などにより、動的に微分します。

\( y = x ^ 2 \) を微分すると \( y' = 2x \) になります。
これは、傾きが 2 の直線の式ですが、これが元の関数の接線の傾きでないことに注意してください。
この直線の式に \( x \) を代入した結果が求めたい傾きになります。

3.2 変数の移動量

微分して算出した傾きによって変数を移動させますが、
その時の移動量は、\( η\cdot\dfrac{dy}{dx} \) とします。
\( η \) （エータ or イーター）はディープラーニングでは学習率と呼ばれ、変数を増減するための係数になります。
以下の実装では、今回は \( η=0.01 \) としています。
この値は、大きいと最小値の谷を飛び越えてしまったり、小さいとなかなか谷に辿り着けなかったりします。
また、学習率に傾きを掛けている理由は、傾きがきつい時は大きく移動して、傾きがゆるくなったら少しずつ移動するため、だと思います。

3.3 ソース

import numpy as np

x = 5        # 初期値（ランダム）
lr = 0.01    # 学習率(learning rate))
gradient = 0 # 勾配（傾き）

for i in range(500):
    
    # 傾きの取得 (y=x^2 を事前に微分して y = 2x にしてある)
    gradient = 2 * x
    
    # ほぼ水平になったら処理を抜けます
    if np.abs(gradient) < 0.1:
        break
    
    # 変数を更新（学習）します
    x = x + lr * gradient * -1 # 傾きとは反対に増減させるため、-1 を掛けています
    
    # 途中経過の出力
    print("{:04}: 傾き={:6.3f}  移動量={:5.3f}  x={:5.3f}".format(
          i,
          round(gradient,3), 
          round(lr * gradient * -1,3), 
          round(x,3)))

実行結果
0000: 傾き = 10.000 移動量 =-0.100  x= 4.900
0001: 傾き = 9.800 移動量 =-0.098  x= 4.802
0002: 傾き = 9.604 移動量 =-0.096  x= 4.706

  ～ 省略 ～

0225: 傾き = 0.106 移動量 =-0.001  x= 0.052
0226: 傾き = 0.104 移動量 =-0.001  x= 0.051
0227: 傾き = 0.102 移動量 =-0.001  x= 0.050
移動量が最初は -0.1 でしたが、最後は -0.001 になっています。
これが、学習率に傾きを掛けている理由です。

また、今回は学習率を 0.01 にしていますが、0.1 にするともっと早く求めることができます。
ディープラーニングでは、学習率のような、人間が調整するパラメーターのことをハイパーパラメーターと呼びます。

4. 勾配降下法の実装 その２

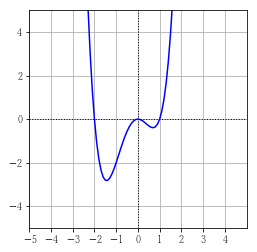
\( y = x^4 + x^3 - 2x^2 \) の最小値を勾配降下法を使用して求めてみます。
ソースは上記とほぼ同じです。
\( x \) の初期値を 4 、
傾きの取得だけ微分した \( y' = 4x^3 + 3x^2 - 4x \) に変更してあります。



import numpy as np

x = 4        # 初期値（ランダム）
lr = 0.01    # 学習率(learning rate))
gradient = 0 # 勾配（傾き）

for i in range(500):
    
    # 傾きの取得 (y=x^4 + x^3 - 2x^2 を事前に微分してある)
    gradient = 4 * x**3 + 3 * x**2 - 4 * x 
    
    # ほぼ水平になったら処理を抜けます
    if np.abs(gradient) < 0.1:
        break
    
    # 変数を更新（学習）します
    x = x + lr * gradient * -1 # 傾きとは反対に増減させるため、-1 を掛けています
    
    # 途中経過の出力
    print("{:04}: 傾き={:6.3f}  移動量={:5.3f}  x={:5.3f}".format(
          i,
          round(gradient, 3),
          round(lr * gradient * -1,3),
          round(x, 3)))

実行結果
0000: 傾き = 288.000 移動量 =-2.880  x= 1.120
0001: 傾き = 4.903 移動量 =-0.049  x= 1.071
0002: 傾き = 4.071 移動量 =-0.041  x= 1.030

  ～ 省略 ～

0042: 傾き = 0.115 移動量 =-0.001  x= 0.711
0043: 傾き = 0.107 移動量 =-0.001  x= 0.709
0044: 傾き = 0.101 移動量 =-0.001  x= 0.708
\( x = 0.708 \) が最小値と言う結果になっていますが、
グラフを見ると、もう片方の谷の極小値になってしまっています。
\( x \) の初期値を -1 や -4 にすると、最小値になります。
このように、勾配降下法は必ずしも最小値にならない可能性があります。

\( x \) の初期値を -4 にした場合の実行結果
0000: 傾き = -192.000 移動量 =1.920  x= -2.080
0001: 傾き = -14.696 移動量 =0.147  x= -1.933
0002: 傾き = -9.950 移動量 =0.100  x= -1.834

  ～ 省略 ～

0027: 傾き = -0.135 移動量 =0.001  x= -1.452
0028: 傾き = -0.118 移動量 =0.001  x= -1.451
0029: 傾き = -0.103 移動量 =0.001  x= -1.450

Tag

New Article