Python - ディープラーニング - 微分
公開日:2019-09-04
更新日:2019-09-04
更新日:2019-09-04
1. 概要
微分とは、関数内の変数が極わずか(無限小)に変化した際に、どのくらい結果が変化するのかを求めるものです。
簡単に言うと、関数をグラフにした際の接線の傾きを求めるのが微分です。
傾きがわかると、関数の結果が増減する方向や量、極大値・極小値などがわかります。

簡単に言うと、関数をグラフにした際の接線の傾きを求めるのが微分です。
傾きがわかると、関数の結果が増減する方向や量、極大値・極小値などがわかります。
2. 動画
3. 微分の定義
関数のある地点での傾きを微分係数と呼び、微分係数を求める関数のことを導関数と呼びます。
そして、関数から導関数を求めることを「微分する」と呼びます。
関数 \( f(x) \) の導関数 \( f'(x) \) は以下のようになります。
分母の \( h \) を 0 にしても計算できる状態に式を変形させて、最後に \( h \) を 0 にして \( lim \) をはずします。
また、\( y = f(x) \) の場合、\( f'(x) \) を \( \dfrac{dy}{dx} \) と書くことがあります。
そして、関数から導関数を求めることを「微分する」と呼びます。
関数 \( f(x) \) の導関数 \( f'(x) \) は以下のようになります。
$$ f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h} $$
分母の \( h \) を 0 にしても計算できる状態に式を変形させて、最後に \( h \) を 0 にして \( lim \) をはずします。
また、\( y = f(x) \) の場合、\( f'(x) \) を \( \dfrac{dy}{dx} \) と書くことがあります。
4. 微分の計算例
4.1 定義に従った微分
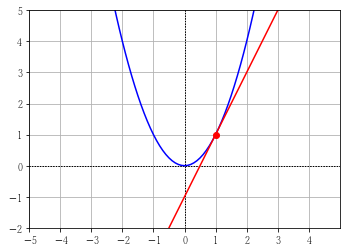
\( f(x) = x^2 \) を微分してみます。
\( f'(x) = 2x \) となりました。引数に 1 を渡すと \( f'(1) = 2 \) となります。
これは、x = 1 の時の \( f(x) \) の接線の傾きが 2 であることを意味します。
また、傾きの符号(±)によって、
引数 \( x \) が増加した際に、元の関数の値が、増加するのか減少するのかがわかります。
プラスの場合は増加、マイナスの場合は減少します。

$$ \begin{eqnarray} f'(x) &=& \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} \\
&=& \lim_{h\to 0}\frac{(x+h)^2-x^2}{h} \\
&=& \lim_{h\to 0}\frac{x^2+2hx+h^2-x^2}{h} \\
&=& \lim_{h\to 0}\frac{2hx+h^2}{h} \\
&=& \lim_{h\to 0}\frac{h(2x+h)}{h} \\
&=& \lim_{h\to 0}(2x+h) \\
&=& 2x
\end{eqnarray} $$
&=& \lim_{h\to 0}\frac{(x+h)^2-x^2}{h} \\
&=& \lim_{h\to 0}\frac{x^2+2hx+h^2-x^2}{h} \\
&=& \lim_{h\to 0}\frac{2hx+h^2}{h} \\
&=& \lim_{h\to 0}\frac{h(2x+h)}{h} \\
&=& \lim_{h\to 0}(2x+h) \\
&=& 2x
\end{eqnarray} $$
\( f'(x) = 2x \) となりました。引数に 1 を渡すと \( f'(1) = 2 \) となります。
これは、x = 1 の時の \( f(x) \) の接線の傾きが 2 であることを意味します。
また、傾きの符号(±)によって、
引数 \( x \) が増加した際に、元の関数の値が、増加するのか減少するのかがわかります。
プラスの場合は増加、マイナスの場合は減少します。

4.2 公式による微分
\( x \) のべき乗は、以下の公式を使って簡単に微分することができます。
また、上記の他にも、簡単に微分するための公式があります。
定義から微分することもできます。
\( (x^n)' = nx^{n-1} \qquad (n=1,2,3,\cdots) \)
\( (x)' = 1 \)
\( (x^2)' = 2x \)
\( (x^3)' = 3x^2 \)
\( (x^4)' = 4x^3 \)
\( (x^{-1})' = -x^{-2} = -\dfrac{1}{x^2}\)
\( (x^{-2})' = -2x^{-3} = -\dfrac{2}{x^3} \)
\( (x^{-3})' = -3x^{-4} = -\dfrac{3}{x^4} \)
\( (a)' = 0 \quad (a は定数) \)
\( (x^2)' = 2x \)
\( (x^3)' = 3x^2 \)
\( (x^4)' = 4x^3 \)
\( (x^{-1})' = -x^{-2} = -\dfrac{1}{x^2}\)
\( (x^{-2})' = -2x^{-3} = -\dfrac{2}{x^3} \)
\( (x^{-3})' = -3x^{-4} = -\dfrac{3}{x^4} \)
\( (a)' = 0 \quad (a は定数) \)
また、上記の他にも、簡単に微分するための公式があります。
定義から微分することもできます。
\( (e^x)' = e^x \)
\( (log\,x)' = \dfrac{1}{x} \quad (x>0) \)
\( (a^x)' = a^x\,log\,a \quad (a>0,\, a\ne1) \)
\( ({sin}\,{x})' = {cos}\,{x} \)
\( ({cos}\,{x})' = -{sin}\,{x} \)
\( ({tan}\,{x})' = \dfrac{1}{{cos^2}\,{x}} \)
\( (log\,x)' = \dfrac{1}{x} \quad (x>0) \)
\( (a^x)' = a^x\,log\,a \quad (a>0,\, a\ne1) \)
\( ({sin}\,{x})' = {cos}\,{x} \)
\( ({cos}\,{x})' = -{sin}\,{x} \)
\( ({tan}\,{x})' = \dfrac{1}{{cos^2}\,{x}} \)
5. 数値微分
コンピューターは、人間が解く方法で微分するのが難しいため、
導関数の \( h \) に微小値を設定し、実際に関数を計算して微分します。
結果は導関数ではなく値となるため、異なる地点の微分係数を取得したい場合は、再度計算する必要があります。
数値微分は以下の式によって行います。
微分したい地点の前後で導関数を計算して平均を取っています。
\( f(x) = x^2 \) が \( x = 1 \) の時の数値微分を行います。
\( h = 0.001 \) とします。
ほぼ 2 となりました。
解析的に微分した \( f'(x) = 2x \) に 1 を入れると 2 となり、ほぼ同じ結果となります。
導関数の \( h \) に微小値を設定し、実際に関数を計算して微分します。
結果は導関数ではなく値となるため、異なる地点の微分係数を取得したい場合は、再度計算する必要があります。
数値微分は以下の式によって行います。
微分したい地点の前後で導関数を計算して平均を取っています。
$$ \begin{eqnarray} f'(x) &=& \frac{1}{2}(\frac{f(x+h)-f(x)}{h}+\frac{f(x)-f(x-h)}{h}) \\
&=& \frac{f(x+h)-f(x-h)}{2h} \\
\end{eqnarray} $$
&=& \frac{f(x+h)-f(x-h)}{2h} \\
\end{eqnarray} $$
\( f(x) = x^2 \) が \( x = 1 \) の時の数値微分を行います。
\( h = 0.001 \) とします。
$$ \begin{eqnarray} f'(1) &=& \frac{f(x+h)-f(x-h)}{2h} \\
&=& \frac{f(1+0.001)-f(1-0.001)}{0.002} \\
&=& \frac{1.001^2 - 0.999^2}{0.002} \\
&=& \frac{1.0020009999999997 - 0.998001}{0.002} \\
&=& \frac{0.0039999999999996705}{0.002} \\
&=& 1.9999999999998352 \\
\end{eqnarray} $$
&=& \frac{f(1+0.001)-f(1-0.001)}{0.002} \\
&=& \frac{1.001^2 - 0.999^2}{0.002} \\
&=& \frac{1.0020009999999997 - 0.998001}{0.002} \\
&=& \frac{0.0039999999999996705}{0.002} \\
&=& 1.9999999999998352 \\
\end{eqnarray} $$
ほぼ 2 となりました。
解析的に微分した \( f'(x) = 2x \) に 1 を入れると 2 となり、ほぼ同じ結果となります。
6. 複雑な関数の微分
6. 1 連鎖律
連鎖律とは、導関数(微分した結果)を分数のように分解して積の形にできる法則です。
これにより、複雑な式を単純な式に分解して微分することができます。
また、以下の変形は数学的には正しくないそうですが、
\( dx \) に微小な値を設定した場合、式としては成り立つようです。
これにより、複雑な式を単純な式に分解して微分することができます。
\( \dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{dx} \)
\( \dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{du} \dfrac{du}{dx} \)
\( \dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{du} \dfrac{du}{dx} \)
また、以下の変形は数学的には正しくないそうですが、
\( dx \) に微小な値を設定した場合、式としては成り立つようです。
\( y = f(x) \)
両辺を \( x \) で微分する。
\( \dfrac{dy}{dx} = f'(x) \)
両辺に \( dx \) を掛ける。
\( dy \fallingdotseq f'(x) \cdot dx = \dfrac{dy}{dx} \cdot dx \)
両辺を \( x \) で微分する。
\( \dfrac{dy}{dx} = f'(x) \)
両辺に \( dx \) を掛ける。
\( dy \fallingdotseq f'(x) \cdot dx = \dfrac{dy}{dx} \cdot dx \)
6.2 連鎖律を使った微分
\( y = (x+1)^2 \) を \( x \) で微分してみます。
まず \( x+1 \) を \( t \) で置き換えて、\( y = (t)^2 \) とします。
そしてこれを \( t \) で微分すると、\( \dfrac{dy}{dt} = 2t \) となります。
次に \( t = x+1 \) を \( x \) で微分すると、\( \dfrac{dt}{dx} = 1 \) となります。
連鎖律により、\( \dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{dx} = 2t \cdot 1 = 2(x+1)\) となります。
\( y = (x+1)^2 \) を展開して微分しても同じ結果になります。
\( y = x^2+2x+1 \) 、\( \dfrac{dy}{dx} = 2x + 2 = 2(x+1) \)
まず \( x+1 \) を \( t \) で置き換えて、\( y = (t)^2 \) とします。
そしてこれを \( t \) で微分すると、\( \dfrac{dy}{dt} = 2t \) となります。
次に \( t = x+1 \) を \( x \) で微分すると、\( \dfrac{dt}{dx} = 1 \) となります。
連鎖律により、\( \dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{dx} = 2t \cdot 1 = 2(x+1)\) となります。
\( y = (x+1)^2 \) を展開して微分しても同じ結果になります。
\( y = x^2+2x+1 \) 、\( \dfrac{dy}{dx} = 2x + 2 = 2(x+1) \)
7. 偏微分(partial differential)
偏微分とは、多変数関数を 1つの変数で微分することです。残りの変数は定数として扱います。
偏微分の記号(\( \partial \))は、パーシャルディーと読みます。他の読み方もいくつかあります。
下記の式を、x, y, z のそれぞれで偏微分してみます。
\( x \) で偏微分
\( y \) で偏微分
\( z \) で偏微分
偏微分の記号(\( \partial \))は、パーシャルディーと読みます。他の読み方もいくつかあります。
下記の式を、x, y, z のそれぞれで偏微分してみます。
\( f(x,y,z)=xy^2+xz^3 \)
\( x \) で偏微分
\( \dfrac{\partial f}{\partial x}(x,y,z) = 1\cdot y^2 + 1\cdot z^3 = y^2+z^3 \)
x は微分すると 1 になるため、y と z がそのまま残ります。\( y \) で偏微分
\( \dfrac{\partial f}{\partial y}(x,y,z) = x \cdot 2y + 0 = 2xy \)
x, z は定数扱いのため、y がない場合は 0 になります。\( z \) で偏微分
\( \dfrac{\partial f}{\partial z}(x,y,z) = 0 + x \cdot 3 z^2 = 3xz^2 \)
8. 全微分
8.1 概要
多変数関数の、全ての変数が少し変化した時の変化量を求めるのが全微分です。
全ての変数で微分した傾き(変化率)ではなく、微小な変化量を求めます。
多変数関数を全ての変数で偏微分して、それぞれに微小の値を掛けて合算した値が全微分となります。
\( f(x,y) \) の全微分
\( f(x,y,z) \) の全微分
変数が増えた場合は、同様に式を増やしていきます。
全ての変数で微分した傾き(変化率)ではなく、微小な変化量を求めます。
多変数関数を全ての変数で偏微分して、それぞれに微小の値を掛けて合算した値が全微分となります。
\( f(x,y) \) の全微分
\( df = \dfrac{\partial f}{\partial x} \cdot dx + \dfrac{\partial f}{\partial y} \cdot dy \)
\( f(x,y,z) \) の全微分
\( df = \dfrac{\partial f}{\partial x} \cdot dx + \dfrac{\partial f}{\partial y} \cdot dy + \dfrac{\partial f}{\partial z} \cdot dz \)
変数が増えた場合は、同様に式を増やしていきます。
8.2 全微分の計算
\( f(x, y) = x + 2y + xy \) の全微分を計算してみます。
まず、全ての変数で偏微分します
偏微分の結果を、全微分の公式にあてはめます。
以上で全微分の計算は完了です。
続いて、実際に値を入れて、定義通りになるか検証してみます。
\( f(x, y) = x + 2y + xy \) に値を代入して結果を算出します
全微分は \( dx, dy \) の分だけ進んだ時の値となるため、
\( f(2, 2) \) に、\( dx = 1, dy = 1 \) とした場合の \( f(2, 2) \) の全微分を加算して、
\( f(3, 3) \) になるか確認してみます。
全微分\( (x = 2, y = 2, dx = 1, dy = 1) \)
\( f(2, 2) + 全微分(x = 2, y = 2, dx = 1, dy = 1) \)
\( f(3, 3) \) は 18 のため、1 足りません。
これは、全微分が微分と同様に、\( dx, dy \) を限りなく小さくした場合の値のためです。
大きくすると、それだけ誤差も大きくなります。
\( dx, dy \) を小さくして誤差が小さくなるか確認してみます。
全微分\( (x = 2, y = 2, dx = 0.1, dy = 0.1) \)
\( dx, dy \) を \( \dfrac{1}{10} \) にしたところ、誤差は \( \dfrac{1}{100} \) になりました。
まず、全ての変数で偏微分します
\( \dfrac{\partial f}{\partial x} = 1 + 0 + y = 1 + y \)
\( \dfrac{\partial f}{\partial y} = 0 + 2 + x = 2 + x \)
\( \dfrac{\partial f}{\partial y} = 0 + 2 + x = 2 + x \)
偏微分の結果を、全微分の公式にあてはめます。
\( df = \dfrac{\partial f}{\partial x} \cdot dx + \dfrac{\partial f}{\partial y} \cdot dy \)
\( \quad = (1 + y) \cdot dx + (2 + x) \cdot dy \)
\( \quad = (1 + y) \cdot dx + (2 + x) \cdot dy \)
以上で全微分の計算は完了です。
続いて、実際に値を入れて、定義通りになるか検証してみます。
\( f(x, y) = x + 2y + xy \) に値を代入して結果を算出します
\( f(0, 0) = 0 + 0 + 0 = 0 \)
\( f(1, 1) = 1 + 2 + 1 = 4 \)
\( f(2, 2) = 2 + 4 + 4 = 10 \)
\( f(3, 3) = 3 + 6 + 9 = 18 \)
\( f(1, 1) = 1 + 2 + 1 = 4 \)
\( f(2, 2) = 2 + 4 + 4 = 10 \)
\( f(3, 3) = 3 + 6 + 9 = 18 \)
全微分は \( dx, dy \) の分だけ進んだ時の値となるため、
\( f(2, 2) \) に、\( dx = 1, dy = 1 \) とした場合の \( f(2, 2) \) の全微分を加算して、
\( f(3, 3) \) になるか確認してみます。
全微分\( (x = 2, y = 2, dx = 1, dy = 1) \)
\( df = (1 + y) \cdot dx + (2 + x) \cdot dy \)
\( \quad = 3 \cdot 1 + (2 + 2) \cdot 1 \)
\( \quad = 7 \)
\( \quad = 3 \cdot 1 + (2 + 2) \cdot 1 \)
\( \quad = 7 \)
\( f(2, 2) + 全微分(x = 2, y = 2, dx = 1, dy = 1) \)
\( f(2, 2) + df = 10 + 7 = 17 \)
\( f(3, 3) \) は 18 のため、1 足りません。
これは、全微分が微分と同様に、\( dx, dy \) を限りなく小さくした場合の値のためです。
大きくすると、それだけ誤差も大きくなります。
\( dx, dy \) を小さくして誤差が小さくなるか確認してみます。
全微分\( (x = 2, y = 2, dx = 0.1, dy = 0.1) \)
\( df = (1 + y) \cdot dx + (2 + x) \cdot dy \)
\( \quad = 3 \cdot 0.1 + 4 \cdot 0.1 \)
\( \quad = 0.3 + 0.4 = 0.7 \)
\( \quad = 3 \cdot 0.1 + 4 \cdot 0.1 \)
\( \quad = 0.3 + 0.4 = 0.7 \)
\( f(2, 2) = 10 \)
\( f(2, 2) + df = 10 + 0.7 = 10.7 \)
\( f(2.1, 2.1) = x + 2y + xy \)
\( \quad = 2.1 + 4.2 + 4.41 = 10.71 \)
\( f(2, 2) + df = 10 + 0.7 = 10.7 \)
\( f(2.1, 2.1) = x + 2y + xy \)
\( \quad = 2.1 + 4.2 + 4.41 = 10.71 \)
\( dx, dy \) を \( \dfrac{1}{10} \) にしたところ、誤差は \( \dfrac{1}{100} \) になりました。

