Python - ディープラーニング - 誤差逆伝播法
公開日:2019-10-01
更新日:2019-10-01
更新日:2019-10-01
1. 概要
勾配降下法を使って損失が最小となる重みとバイアスを取得することができますが、単純にニューラルネットワークを何度も数値微分すると、処理にかなり時間がかかります。
そこで、誤差逆伝播法(Backpropagation)を使うと、少ない計算で微分することができます。
微分がわからない場合は、こちらをご確認ください。
また、今回はソフトマックス関数とクロスエントロピー誤差の逆伝播の説明は省略して、結果だけ使用します。
そこで、誤差逆伝播法(Backpropagation)を使うと、少ない計算で微分することができます。
微分がわからない場合は、こちらをご確認ください。
また、今回はソフトマックス関数とクロスエントロピー誤差の逆伝播の説明は省略して、結果だけ使用します。
2. 動画
3. 基本
誤差逆伝播法とは、1度出力層まで計算を行い、各ノードの結果と重みを使って、後方(右側)から先頭(左側)に向かって微分を行う方法です。
以下の構成で考えてみます。

まずは出力層まで順番に計算を行います。
ディープラーニングでは、損失関数を重みで微分して、勾配降下法により適切な重みを見つけます。
そのため次は、出力値(\( E \))を各重みで微分します。
式に重みが直接含まれていない場合は、連鎖律による変形をして微分します。
まとめると以下のようになります。
この結果を見るとわかりますが、法則があることがわかります。
微分する重みの前の層のノードの値と、
微分する重みのそれ以降の重みを全て掛け合わせたものが微分した結果になっています。
見方を変えると、順方向とは逆側から重みを掛けていき、
微分する重みの前のノードの値を掛けた値が微分の結果になります。
例えば \( \dfrac{dE}{dw2} \) は、後方から \( w4 \)、\( w3 \) と掛けていき、
\( w2 \) になったら、\( w2 \) は掛けずに、その前のノードの値 \( B \) を掛けたものが微分の結果になります。

以下の構成で考えてみます。

まずは出力層まで順番に計算を行います。
\( B = w1 \cdot A \)
\( C = w2 \cdot B \)
\( D = w3 \cdot C \)
\( E = w4 \cdot D \)
\( C = w2 \cdot B \)
\( D = w3 \cdot C \)
\( E = w4 \cdot D \)
ディープラーニングでは、損失関数を重みで微分して、勾配降下法により適切な重みを見つけます。
そのため次は、出力値(\( E \))を各重みで微分します。
式に重みが直接含まれていない場合は、連鎖律による変形をして微分します。
\( \dfrac{dE}{dw1} = \dfrac{dE}{dD} \dfrac{dD}{dw1} = w4 \cdot \dfrac{dD}{dw1} \)
\( \dfrac{dD}{dw1} = \dfrac{dD}{dC} \dfrac{dC}{dw1} = w3 \cdot \dfrac{dC}{dw1} \)
\( \dfrac{dC}{dw1} = \dfrac{dC}{dB} \dfrac{dB}{dw1} = w2 \cdot \dfrac{dB}{dw1} = w2 \cdot A \)
\( \dfrac{dD}{dw1} = \dfrac{dD}{dC} \dfrac{dC}{dw1} = w3 \cdot \dfrac{dC}{dw1} \)
\( \dfrac{dC}{dw1} = \dfrac{dC}{dB} \dfrac{dB}{dw1} = w2 \cdot \dfrac{dB}{dw1} = w2 \cdot A \)
まとめると以下のようになります。
\( \dfrac{dE}{dw1} = \dfrac{dE}{dD} \dfrac{dD}{dC} \dfrac{dC}{dB} \dfrac{dB}{dw1} = w4 \cdot w3 \cdot w2 \cdot A \)
\( \dfrac{dE}{dw2} = \dfrac{dE}{dD} \dfrac{dD}{dC} \dfrac{dC}{dw2} = w4 \cdot w3 \cdot B \)
\( \dfrac{dE}{dw3} = \dfrac{dE}{dD} \dfrac{dD}{dw3} = w4 \cdot C \)
\( \dfrac{dE}{dw4} = \dfrac{dE}{dw4} = D \)
\( \dfrac{dE}{dw2} = \dfrac{dE}{dD} \dfrac{dD}{dC} \dfrac{dC}{dw2} = w4 \cdot w3 \cdot B \)
\( \dfrac{dE}{dw3} = \dfrac{dE}{dD} \dfrac{dD}{dw3} = w4 \cdot C \)
\( \dfrac{dE}{dw4} = \dfrac{dE}{dw4} = D \)
この結果を見るとわかりますが、法則があることがわかります。
微分する重みの前の層のノードの値と、
微分する重みのそれ以降の重みを全て掛け合わせたものが微分した結果になっています。
見方を変えると、順方向とは逆側から重みを掛けていき、
微分する重みの前のノードの値を掛けた値が微分の結果になります。
例えば \( \dfrac{dE}{dw2} \) は、後方から \( w4 \)、\( w3 \) と掛けていき、
\( w2 \) になったら、\( w2 \) は掛けずに、その前のノードの値 \( B \) を掛けたものが微分の結果になります。
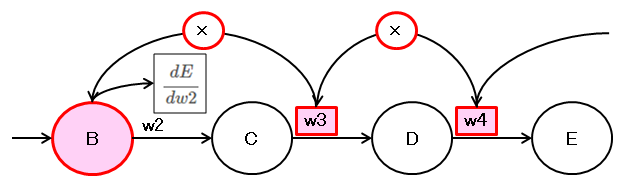
4. 複数経路のサンプル1
以下の構成を各重みで微分してみます。

まずは \( C \) を \( w3 \) と \( w4 \) で微分します。
これは \( C \) から重みが直接見えているため、普通に微分できます。
続いて、\( w1 \) と \( w2 \) で微分します。
まずは \( w1 \) で微分
同様に、\( w2 \) で微分
経路が2つになりましたが、先ほどの法則に当てはまります。
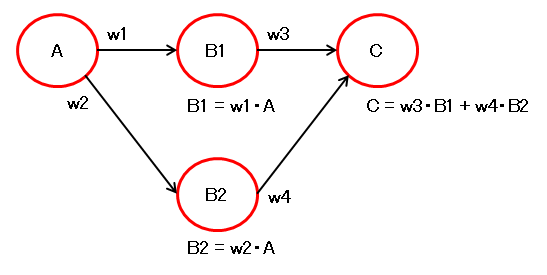
まずは \( C \) を \( w3 \) と \( w4 \) で微分します。
これは \( C \) から重みが直接見えているため、普通に微分できます。
\( C = w3 \cdot B1 + w4 \cdot B2 \)
\( \dfrac{dC}{dw3} = B1 + 0 = B1 \)
\( \dfrac{dC}{dw4} = 0 + B2 = B2 \)
\( \dfrac{dC}{dw3} = B1 + 0 = B1 \)
\( \dfrac{dC}{dw4} = 0 + B2 = B2 \)
続いて、\( w1 \) と \( w2 \) で微分します。
まずは \( w1 \) で微分
\( C = w3 \cdot B1 + w4 \cdot B2 \)
\( \dfrac{dC}{dw1} = w3 \cdot \dfrac{dB1}{dw1} + w4 \cdot \dfrac{dB2}{dw1} \)
\( \dfrac{dB1}{dw1} = A、\quad \dfrac{dB2}{dw1} = 0 \quad のため、\)
\( \dfrac{dC}{dw1} = w3 \cdot A + w4 \cdot 0 = w3 \cdot A \)
\( \dfrac{dC}{dw1} = w3 \cdot \dfrac{dB1}{dw1} + w4 \cdot \dfrac{dB2}{dw1} \)
\( \dfrac{dB1}{dw1} = A、\quad \dfrac{dB2}{dw1} = 0 \quad のため、\)
\( \dfrac{dC}{dw1} = w3 \cdot A + w4 \cdot 0 = w3 \cdot A \)
同様に、\( w2 \) で微分
\( \dfrac{dC}{dw2} = w3 \cdot 0 + w4 \cdot A = w4 \cdot A \)
経路が2つになりましたが、先ほどの法則に当てはまります。
5. 複数経路のサンプル2
以下の構成で微分してみます。

\( D \) を \( w1 \) で微分します。
\( C1 \) を \( w1 \) で微分します。
\( B1 \) と \( B2 \) を \( w1 \) で微分します。
よって、
同様に、\( C2 \) を \( w1 \) で微分します。
よって、
\( w1 \) を通る経路は、
\( D \) → \( C1 \) → \( B1 \) → \( A1 \) と、
\( D \) → \( C2 \) → \( B1 \) → \( A1 \) の、
2つありますが、各径路の微分結果を見ると、法則に当てはまることがわかります。
複数経路ある場合の微分は、微分する重みを含む全経路を法則によって微分して、それらを合算すれば良さそうです。
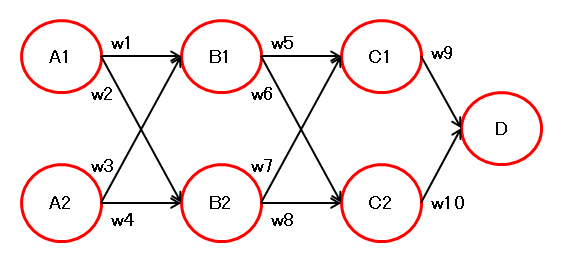
\( D \) を \( w1 \) で微分します。
\( D = w9 \cdot C1 + w10 \cdot C2 \)
\( \dfrac{dD1}{dw1} = w9 \cdot \dfrac{dC1}{dw1} + w10 \cdot \dfrac{dC2}{dw1} \)
\( \dfrac{dD1}{dw1} = w9 \cdot \dfrac{dC1}{dw1} + w10 \cdot \dfrac{dC2}{dw1} \)
\( C1 \) を \( w1 \) で微分します。
\( C1 = w5 \cdot B1 + w7 \cdot B2 \)
\( \dfrac{dC1}{dw1} = w5 \cdot \dfrac{dB1}{dw1} + w7 \cdot \dfrac{dB2}{dw1} \)
\( \dfrac{dC1}{dw1} = w5 \cdot \dfrac{dB1}{dw1} + w7 \cdot \dfrac{dB2}{dw1} \)
\( B1 \) と \( B2 \) を \( w1 \) で微分します。
\( B1 = w1 \cdot A1 + w3 \cdot A2 \)
\( \dfrac{dB1}{dw1} = A1 + 0 = A1 \)
\( B2 = w2 \cdot A1 + w4 \cdot A2 \)
\( \dfrac{dB2}{dw1} = 0 + 0 = 0 \)
\( \dfrac{dB1}{dw1} = A1 + 0 = A1 \)
\( B2 = w2 \cdot A1 + w4 \cdot A2 \)
\( \dfrac{dB2}{dw1} = 0 + 0 = 0 \)
よって、
\( \dfrac{dC1}{dw1} = w5 \cdot A1 + w7 \cdot 0 = w5 \cdot A1 \)
同様に、\( C2 \) を \( w1 \) で微分します。
\( C2 = w6 \cdot B1 + w8 \cdot B2 \)
\( \dfrac{dC2}{dw1} = w6 \cdot \dfrac{dB1}{dw1} + w8 \cdot \dfrac{dB2}{dw1} = w6 \cdot A1 \)
\( \dfrac{dC2}{dw1} = w6 \cdot \dfrac{dB1}{dw1} + w8 \cdot \dfrac{dB2}{dw1} = w6 \cdot A1 \)
よって、
\( \dfrac{dD1}{dw1} = w9 \cdot w5 \cdot A1 + w10 \cdot w6 \cdot A1 \)
\( w1 \) を通る経路は、
\( D \) → \( C1 \) → \( B1 \) → \( A1 \) と、
\( D \) → \( C2 \) → \( B1 \) → \( A1 \) の、
2つありますが、各径路の微分結果を見ると、法則に当てはまることがわかります。
複数経路ある場合の微分は、微分する重みを含む全経路を法則によって微分して、それらを合算すれば良さそうです。
6. 複数経路のサンプル3
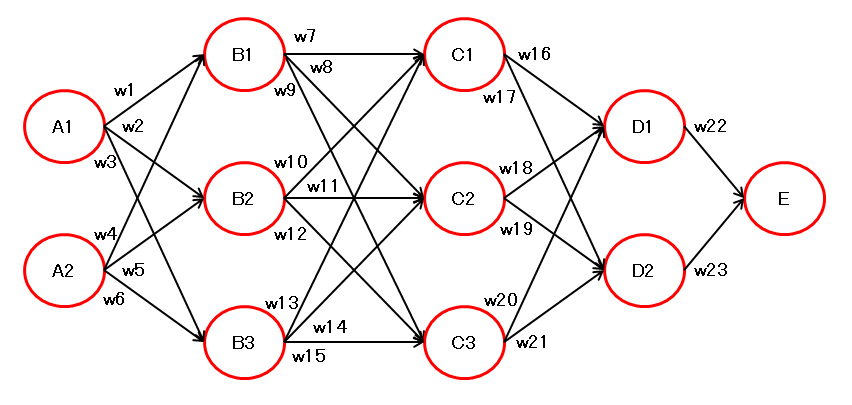
以下の構成の \( E \) を \( w1 \) で微分します。

\( w1 \) を通る経路は以下の6通りです。
\( E \) → \( D1 \) → \( C1 \) → \( B1 \) → \( A1 \)
\( E \) → \( D1 \) → \( C2 \) → \( B1 \) → \( A1 \)
\( E \) → \( D1 \) → \( C3 \) → \( B1 \) → \( A1 \)
\( E \) → \( D2 \) → \( C1 \) → \( B1 \) → \( A1 \)
\( E \) → \( D2 \) → \( C2 \) → \( B1 \) → \( A1 \)
\( E \) → \( D2 \) → \( C3 \) → \( B1 \) → \( A1 \)
法則に従って微分すると以下のようになります。
\( w1 \) を増加させた際に、微分結果の分だけ増加するのか検証します。
実行結果
\( w1 \) を通る経路は以下の6通りです。
\( E \) → \( D1 \) → \( C1 \) → \( B1 \) → \( A1 \)
\( E \) → \( D1 \) → \( C2 \) → \( B1 \) → \( A1 \)
\( E \) → \( D1 \) → \( C3 \) → \( B1 \) → \( A1 \)
\( E \) → \( D2 \) → \( C1 \) → \( B1 \) → \( A1 \)
\( E \) → \( D2 \) → \( C2 \) → \( B1 \) → \( A1 \)
\( E \) → \( D2 \) → \( C3 \) → \( B1 \) → \( A1 \)
法則に従って微分すると以下のようになります。
\( \dfrac{dE}{dw1} = w22 \cdot w16 \cdot w7 \cdot A1 \quad + \)
\( \qquad \qquad w22 \cdot w18 \cdot w8 \cdot A1 \quad + \)
\( \qquad \qquad w22 \cdot w20 \cdot w9 \cdot A1 \quad + \)
\( \qquad \qquad w23 \cdot w17 \cdot w7 \cdot A1 \quad + \)
\( \qquad \qquad w23 \cdot w19 \cdot w8 \cdot A1 \quad + \)
\( \qquad \qquad w23 \cdot w21 \cdot w9 \cdot A1 \)
\( \qquad \qquad w22 \cdot w18 \cdot w8 \cdot A1 \quad + \)
\( \qquad \qquad w22 \cdot w20 \cdot w9 \cdot A1 \quad + \)
\( \qquad \qquad w23 \cdot w17 \cdot w7 \cdot A1 \quad + \)
\( \qquad \qquad w23 \cdot w19 \cdot w8 \cdot A1 \quad + \)
\( \qquad \qquad w23 \cdot w21 \cdot w9 \cdot A1 \)
\( w1 \) を増加させた際に、微分結果の分だけ増加するのか検証します。
import numpy as np
# ニューラルネットワークの計算
def calc(layer1_val, layer1_w, layer2_w, layer3_w, layer4_w):
layer2_val = np.dot(layer1_val, layer1_w)
layer3_val = np.dot(layer2_val, layer2_w)
layer4_val = np.dot(layer3_val, layer3_w)
layer5_val = np.dot(layer4_val, layer4_w)
return layer5_val[0]
# 入力値
layer1_val = np.array([1, 2])
# 重み
w1, w2, w3, w4, w5 = 1, 2, 3, 4, 5
w6 ,w7, w8, w9, w10 = 6, 7, 8, 9,10
w11,w12,w13,w14,w15 = 11,12,13,14,15
w16,w17,w18,w19,w20 = 16,17,18,19,20
w21,w22,w23 = 21,22,23
# レイヤーごとの重み
layer1_w = np.array([[w1, w2, w3],
[w4, w5, w6]])
layer2_w = np.array([[w7, w8, w9],
[w10, w11, w12],
[w13, w14, w15]])
layer3_w = np.array([[w16, w17],
[w18, w19],
[w20, w21]])
layer4_w = np.array([[w22],
[w23]])
# 計算 1回目
result1 = calc(layer1_val, layer1_w, layer2_w, layer3_w, layer4_w)
print(result1, "1回目の計算結果")
# w1 で微分
a1 = layer1_val[0]
dw1 = w22 * w16 * w7 * a1 + \
w22 * w18 * w8 * a1 + \
w22 * w20 * w9 * a1 + \
w23 * w17 * w7 * a1 + \
w23 * w19 * w8 * a1 + \
w23 * w21 * w9 * a1
print(" ", dw1, "w1の微分結果")
# w1 を 1 増加させる
layer1_w[0, 0] += 1
# 計算 2回目
result2 = calc(layer1_val, layer1_w, layer2_w, layer3_w, layer4_w)
print(result2 , "2回目の計算結果(w1増加後)" )
print(result1 + dw1, "1回目の計算結果 + w1の微分結果")
実行結果
1041066 1回目の計算結果
20172 w1の微分結果
1061238 2回目の計算結果(w1増加後)
1061238 1回目の計算結果 + w1の微分結果
7. バイアスの誤差逆伝播
以下の構成の \( D \) を バイアスの \( b1 \) で微分します。

\( D \) を \( b1 \) で微分します。
\( C1 \) を \( b1 \) で微分します。
\( C2 \) を \( b1 \) で微分します。
よって、
同様に、
バイアスの場合は、各経路の重みの積の合計になります。
前の層の出力値を使わない点が、重みの場合と異なります。
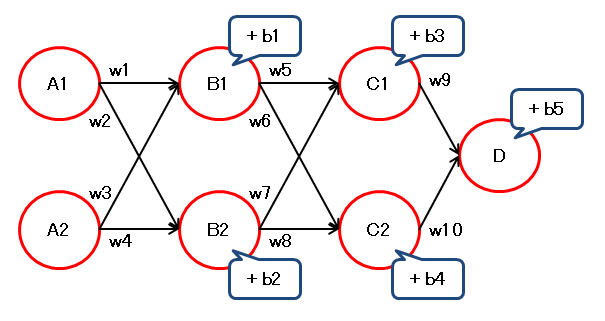
\( D \) を \( b1 \) で微分します。
\( D = w9 \cdot C1 + w10 \cdot C2 + b5 \)
\( \dfrac{dD1}{db1} = w9 \cdot \dfrac{dC1}{db1} + w10 \cdot \dfrac{dC2}{db1} \)
\( \dfrac{dD1}{db1} = w9 \cdot \dfrac{dC1}{db1} + w10 \cdot \dfrac{dC2}{db1} \)
\( C1 \) を \( b1 \) で微分します。
\( C1 = w5 \cdot B1 + w7 \cdot B2 + b3 \)
\( \dfrac{dC1}{db1} = w5 \cdot \dfrac{dB1}{db1} + w7 \cdot \dfrac{dB2}{db1} \)
\( \qquad = w5 \cdot 1 + w7 \cdot 0 = w5 \)
\( \dfrac{dC1}{db1} = w5 \cdot \dfrac{dB1}{db1} + w7 \cdot \dfrac{dB2}{db1} \)
\( \qquad = w5 \cdot 1 + w7 \cdot 0 = w5 \)
\( C2 \) を \( b1 \) で微分します。
\( C2 = w6 \cdot B1 + w8 \cdot B2 + b3 \)
\( \dfrac{dC2}{db1} = w6 \cdot \dfrac{dB1}{db1} + w8 \cdot \dfrac{dB2}{db1} \)
\( \qquad = w6 \cdot 1 + w8 \cdot 0 = w6 \)
\( \dfrac{dC2}{db1} = w6 \cdot \dfrac{dB1}{db1} + w8 \cdot \dfrac{dB2}{db1} \)
\( \qquad = w6 \cdot 1 + w8 \cdot 0 = w6 \)
よって、
\( \dfrac{dD1}{db1} = w9 \cdot w5 + w10 \cdot w6 \)
となります。同様に、
\( \dfrac{dD1}{db2} = w9 \cdot w7 + w10 \cdot w8 \)
となります。バイアスの場合は、各経路の重みの積の合計になります。
前の層の出力値を使わない点が、重みの場合と異なります。
8. 誤差逆伝播法の実装
誤差逆伝播法を使用して、数値微分を行わずに、論理演算(XOR)の再現を行います。
また、ソフトマックス関数と損失関数(クロスエントロピー誤差)を合わせた場合に逆伝播する値は、「結果-正解」になります。
また、ソフトマックス関数と損失関数(クロスエントロピー誤差)を合わせた場合に逆伝播する値は、「結果-正解」になります。
import numpy as np
import matplotlib.pyplot as plt
def relu(lst):
lst[lst <= 0] = 0
return lst
# ソフトマックス関数(ndarray版)
def softmax(x):
# max() と sum() で次元が減り、
# 元の x と直接計算ができなくなるため、転置(行列の入替)しておきます
x = x.T
# オーバーフロー対策。最大値が0になり、他はマイナスになる。
x = x - np.max(x, axis = 0)
# ソフトマックス
y = np.exp(x) / np.sum(np.exp(x), axis = 0)
return y.T #転置していたので元に戻して返す
# クロスエントロピー誤差の取得
def cross_entropy_error(y, t):
size = y.shape[0]
loss = 0
for i in range(size):
# 値 1 のインデックスを取得します
idx = t[i].argmax()
# 損失を加算します
loss = loss + np.log(y[i, idx] + 1e-7)
loss = - loss / size
return loss
# 予測します
# ニューラルネットワークの計算を行い、ソフトマックスで結果を返す
def predict(v1, w1, b1, w2, b2):
v2 = np.dot(v1, w1) + b1
v2 = relu(v2)
v3 = np.dot(v2, w2) + b2
return np.argmax(softmax(v3))
def get_weight(v1, w1, b1, w2, b2, t_value):
data_count = t_value.shape[0]
c = 0
for i in range(5000):
#--------------------
# 順方向
#--------------------
v2 = np.dot(v1, w1) + b1
v2_org = v2.copy() #誤差逆伝播で使用
v2 = relu(v2)
v3 = np.dot(v2, w2) + b2
softmax_result = softmax(v3)
# 現在の損失率とグラフの表示
if c % 100 == 0:
draw_graph(w1, b1, w2, b2)
print("損失率", cross_entropy_error(softmax_result, t_value))
c = 0
c = c + 1
#--------------------
# 誤差逆伝播
#--------------------
# 「ソフトマックス + クロスエントロピー誤差」が逆伝播する値は「結果 - 正解」になる
# 学習データ毎の誤差をあとで合算するため、事前に誤差をデータ数で割る
gosa = (softmax_result - t_value) / data_count
# 重みとバイアスの微分
dw2 = np.dot(v2.T, gosa)
db2 = np.sum(gosa, axis = 0)
#誤差に重みをかけて、前の層へ誤差を伝播していきます
gosa = np.dot(gosa, w2.T)
# ReLU で値が 0 になっていた場合は、誤差を 0 にします
gosa[v2_org <= 0] = 0
# 重みとバイアスの微分
dw1 = np.dot(v1.T, gosa)
db1 = np.sum(gosa, axis = 0)
#誤差に重みをかけて、前の層へ誤差を伝播していきます
# gosa = np.dot(gosa, w1.T)
#--------------------
# 重みとバイアスの更新
#--------------------
learning_rate = 0.01 # 学習率
w1 -= dw1 * learning_rate
w2 -= dw2 * learning_rate
b1 -= db1 * learning_rate
b2 -= db2 * learning_rate
return (w1, b1, w2, b2)
# グラフの描画
def draw_graph(w1, b1, w2, b2):
plt.grid() # グリッド表示
plt.xlim([-1.5, 1.5]) # グラフ描画範囲(X軸)
plt.ylim([-1.5, 1.5]) # グラフ描画範囲(Y軸)
# グラフ描画
x_list = np.arange(-1, 1.6, 0.1) # x軸
y_list = np.arange(-1, 1.6, 0.1) # y軸
for y in y_list:
for x in x_list:
p = predict(np.array([x, y]), w1, b1, w2, b2)
if p == 1:
plt.scatter(x, y, c = 'b')
plt.show()
print("{0} {1} {2} {3}".format(
predict(np.array([0, 0]), w1, b1, w2, b2),
predict(np.array([0, 1]), w1, b1, w2, b2),
predict(np.array([1, 0]), w1, b1, w2, b2),
predict(np.array([1, 1]), w1, b1, w2, b2)))
#--------------------
# メイン
#--------------------
# 重みとバイアス
w1 = np.random.randn( 2, 16) * 0.1
w2 = np.random.randn(16, 2) * 0.1
b1 = np.zeros(16)
b2 = np.zeros(2)
# 入力データ(論理演算の全組み合わせ)
input_value = np.array([
[0, 0],
[0, 1],
[1, 0],
[1, 1],
])
# 正解データ(one-hot表現)
t_value = np.array([
[1, 0],
[0, 1],
[0, 1],
[1, 0],
])
# 適切な重みとバイアスの取得
(w1, b1, w2, b2) = get_weight(input_value, w1, b1, w2, b2, t_value)

