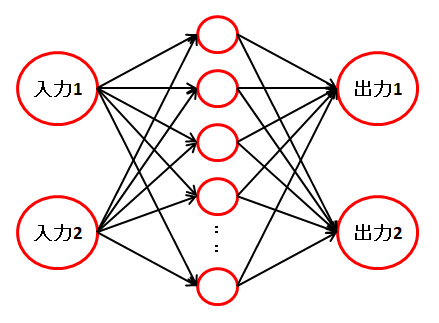
以下のニューラルネットワークを使用して、論理演算を再現します。



損失が最小となる重みとバイアスを求めるため、今回の勾配降下法の対象となる関数は、 各ノードの計算を行い、ソフトマックス関数と損失関数（クロスエントロピー誤差）を通した、ニューラルネットワーク全体が対象となります。

そして、全ての重みとバイアスの数だけ編微分を行い、重みとバイアスを更新していきます。

import matplotlib.pyplot as plt
import numpy as np

# ReLU(ndarray版)
def relu(lst):
    lst[lst <= 0] = 0
    return lst


# ソフトマックス関数(ndarray版)
def softmax(x):
    #転置しない場合のやり方
    #x2 = x.copy()
    #x2 = x2 - np.max(x2, axis = 1).reshape(x2.shape[0], 1)
    #y2 = np.exp(x2) / np.sum(np.exp(x2), axis = 1).reshape(x2.shape[0], 1) 
    
    
    # max() と sum() で次元が減り、
    # 元の x と直接計算ができなくなるため、転置（行列の入替）しておきます
    x = x.T
    
    # オーバーフロー対策。最大値が0になり、他はマイナスになる。
    x = x - np.max(x, axis = 0)
    
    # ソフトマックス
    y = np.exp(x) / np.sum(np.exp(x), axis = 0)
    
    return y.T #転置していたので元に戻して返す


# クロスエントロピー誤差の取得
def cross_entropy_error(y, t):
    size = y.shape[0]
    
    loss = 0
    for i in range(size):
        # 正解データ(one-hot)の 1 になっているインデックスを取得します
        idx = t[i].argmax()
        
        # 損失を加算します(正解データの 1 の予測結果だけを使う)
        loss = loss + np.log(y[i, idx] + 1e-7)
    
    loss = - loss / size
       
    return loss


# 予測します
# ニューラルネットワークの計算を行い、ソフトマックスで結果を返す
def predict(v1, w1, b1, w2, b2):
    v2 = np.dot(v1, w1) + b1
    v2 = relu(v2)
    
    v3 = np.dot(v2, w2) + b2
    return softmax(v3)


# 損失の取得
def get_loss(v, w1, b1, w2, b2, t_value):
    
    # 予測(分類)します
    result = predict(v, w1, b1, w2, b2)
    
    # 損失を取得します
    loss = cross_entropy_error(result, t_value)
    return loss


# 勾配降下法による学習
def gradient_descent(v1, w1, b1, w2, b2, t_value):
    h = 0.1
    
    # 重みの微分
    dw1 = np.zeros_like(w1) # w1 と同じサイズの配列の作成
    org_w1 = w1.copy() # h を増減した値を戻すのに使用
    for i in range(w1.shape[0]):
        for j in range(w1.shape[1]):
            # 数値微分 f(x+h)-f(x-h)/2h
            w1[i, j] = org_w1[i, j] + h
            f1 = get_loss(v1, w1, b1, w2, b2, t_value)
            
            w1[i, j] = org_w1[i, j] - h
            f2 = get_loss(v1, w1, b1, w2, b2, t_value)
            
            dw1[i, j] = (f1 - f2) / (h * 2)
            
            # 元に戻す
            w1[i, j] = org_w1[i, j]
    
    # 重みの微分        
    dw2 = np.zeros_like(w2)
    org_w2 = w2.copy()
    for i in range(w2.shape[0]):
        for j in range(w2.shape[1]):
            w2[i, j] = org_w2[i, j] + h
            f1 = get_loss(v1, w1, b1, w2, b2, t_value)
            
            w2[i, j] = org_w2[i, j] - h
            f2 = get_loss(v1, w1, b1, w2, b2, t_value)
            
            dw2[i, j] = (f1 - f2) / (h * 2)
            
            w2[i, j] = org_w2[i, j]
            
    # バイアスの微分
    db1 = np.zeros_like(b1)
    org_b1 = b1.copy()
    for i in range(b1.shape[0]):
        b1[i] = org_b1[i] + h ; f1 = get_loss(v1, w1, b1, w2, b2, t_value)
        b1[i] = org_b1[i] - h ; f2 = get_loss(v1, w1, b1, w2, b2, t_value)
        db1[i] = (f1 - f2) / (h * 2)
        b1[i] = org_b1[i]

    # バイアスの微分
    db2 = np.zeros_like(b2)
    org_b2 = b2.copy()
    for i in range(b2.shape[0]):
        b2[i] = org_b2[i] + h ; f1 = get_loss(v1, w1, b1, w2, b2, t_value)
        b2[i] = org_b2[i] - h ; f2 = get_loss(v1, w1, b1, w2, b2, t_value)
        db2[i] = (f1 - f2) / (h * 2)
        b2[i] = org_b2[i]
        
    # 重みの学習
    lr = 0.01
    for i in range(w1.shape[0]):
        for j in range(w1.shape[1]):
            w1[i, j] = w1[i, j] + lr * dw1[i, j] * -1
            
    for i in range(w2.shape[0]):
        for j in range(w2.shape[1]):
            w2[i, j] = w2[i, j] + lr * dw2[i, j] * -1

    # バイアスの学習
    b1 = b1 + lr * db1 * -1
    b2 = b2 + lr * db2 * -1
    
    return w1, b1, w2, b2


## グラフの描画
def draw_graph(w1, b1, w2, b2):
    plt.grid()            # グリッド表示
    plt.xlim([-1.5, 1.5]) # グラフ描画範囲(X軸)
    plt.ylim([-1.5, 1.5]) # グラフ描画範囲(Y軸)
    
    # グラフ描画
    x_list = np.arange(-1, 1.6, 0.1) # x軸
    y_list = np.arange(-1, 1.6, 0.1) # y軸
    for y in y_list:
        for x in x_list:
            p = np.argmax(predict(np.array([x, y]), w1, b1, w2, b2))
            if p == 1:
                plt.scatter(x, y, c = 'b')
                
    plt.show()
    
    print("{0} {1} {2} {3}".format(
        np.argmax(predict(np.array([0, 0]), w1, b1, w2, b2)),
        np.argmax(predict(np.array([0, 1]), w1, b1, w2, b2)),
        np.argmax(predict(np.array([1, 0]), w1, b1, w2, b2)),
        np.argmax(predict(np.array([1, 1]), w1, b1, w2, b2))))
    


# ここからメイン

# 重み
w1 = np.random.randn(2, 8) * 0.1 #入力数:2 中間のノード数:8
w2 = np.random.randn(8, 2) * 0.1 #        中間のノード数:8 出力数:2

# バイアス
b1 = np.zeros(8)
b2 = np.zeros(2)

# 入力データ(論理演算の全ての組み合わせ)
input_value = np.array([
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1]
])
    
# 正解データ(XOR) one-hot表現
t_value = np.array([
    [1, 0], # 0
    [0, 1], # 1
    [0, 1], # 1
    [1, 0]  # 0
])

# 勾配降下法による学習
c = 0 # グラフ描画用のカウント
for i in range(5001): 
    # 勾配降下法による学習
    w1, b1, w2, b2 = gradient_descent(input_value, w1, b1, w2, b2, t_value)
    
    if c % 100 == 0:
        draw_graph(w1, b1, w2, b2)
        c = 0
    
    c = c + 1