Python - ディープラーニング - 概要

公開日：2019-08-21 更新日：2019-08-21
[Python]

1. 概要

ディープラーニング（深層学習）の概要についてです。

2. 動画



【訂正】
19:55 付近で、出力値に対して正解（教師データ）を教えると説明していますが、
正しくは、入力値（大きさ、色、角の数）に対して、正解を教えてあげます。

3. 機械学習とディープラーニング（深層学習）の関係について

機械学習は、値の分類や推測を、学習するアルゴリズムを使って行うものです。
アルゴリズムとしては、SVM、ランダムフォレスト、k-NN（k近傍法）など、様々なものがありますが、 ディープラーニングもそのアルゴリズムのうちの１つになります。
ディープラーニングは、ニューラルネットワークで学習をするアルゴリズムにより問題を解決します。

4. ニューラルネットワーク（神経網）

ニューラルネットワークとは、脳にある神経を伝達するネットワークを数学的に表現したモデルです。

4.1 単純パーセプトロン

入力層と出力層だけの構造です。
複数の入力から、値を１つ出力します。


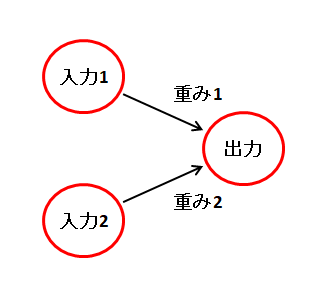
出力値は以下のようになります。
出力 = 活性化関数(入力1 * 重み1 + 入力2 * 重み2 + バイアス) 

活性化関数の例（ステップ関数）
  引数 <= 0 なら 0
  引数 >  0 なら 1
活性化関数で出力値を調整します。
ここに出てくる重みとバイアスを適切な値になるように学習するのがディープラーニングです。

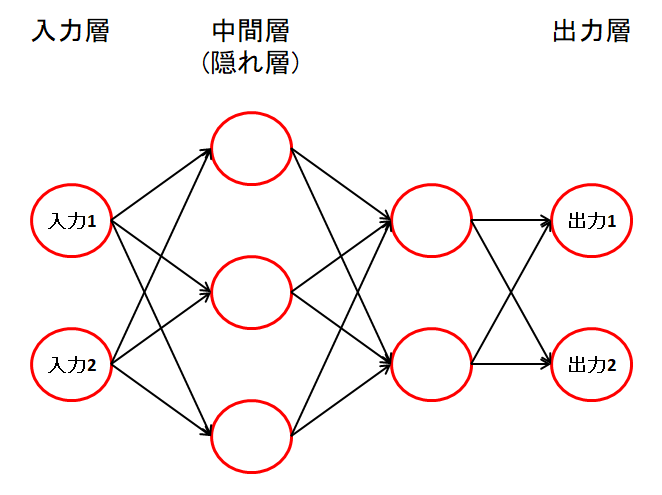
4.2 多層パーセプトロン

入力層と出力層の間に、いくつかの中間層（隠れ層）を追加したものが、多層パーセプトロンです。
各ノード（ニューロン）の計算は、単純パーセプトロンと同じです。



5. 活性化関数について

活性化関数は、出力値を調整する関数です。

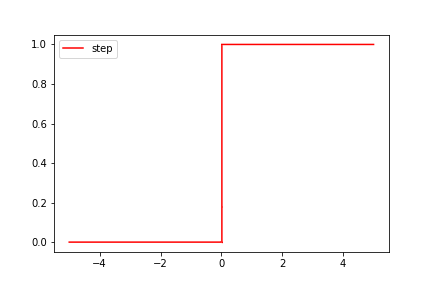
5.1 ステップ関数

単純パーセプトロンで使用します。
$$
f(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
0\:\:(x \leqq 0)\\
1\:\:(x \gt 0)
\end{array}
\right.
\end{eqnarray}
$$



5.2 シグモイド関数

どんな値を入れても、0 ～ 1 の範囲に収めて出力します。
大きな＋の値を入れると 1 となり、
大きな－の値を入れると 0 になります。

$$ f(x)=\dfrac{1}{1+e^{-x}}\ $$
e^-x は、numpy.exp(-x) で算出できます。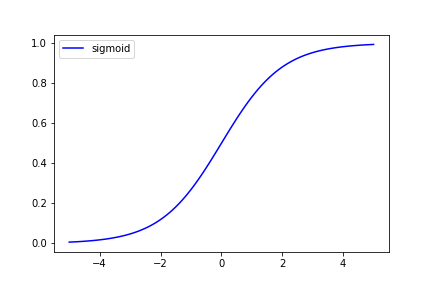



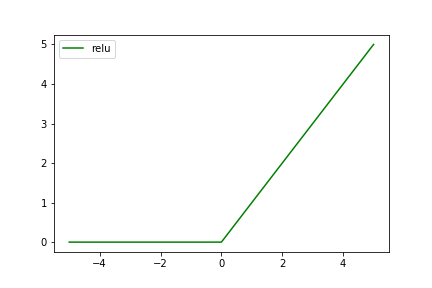
5.3 ReLU関数（Rectified Linear Unit）

グラフの形が傾斜（ramp）になってるため、ランプ関数とも呼びます。
$$
f(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
0\:\:(x \leqq 0)\\
x\:\:(x \gt 0)
\end{array}
\right.
\end{eqnarray}
$$



5.4 ソフトマックス関数

分類問題の出力層で使います。
出力値の各要素は 0 ～ 1 の範囲となり、全要素の合計は 1 になります。
他の活性化関数と異なり、各ノードの計算で、全てのノードの値を使用します。
各ノードで計算して、一番大きい値のノードが、判別された分類となります。
そのため、出力層のノード数は、分類の数だけ用意する必要があります。

$$
f(k)=\dfrac{e^{N_k}}{\sum_{i=1}^n e^{N_i}}\ $$
$$
n：出力層のノード数
$$ $$
k：出力層のノード番号
$$ $$
N_1 ～ N_n：ノードの値
$$

出力ノードが３つの場合のイメージです。わかりやすくするため、\( e \) を省いています。


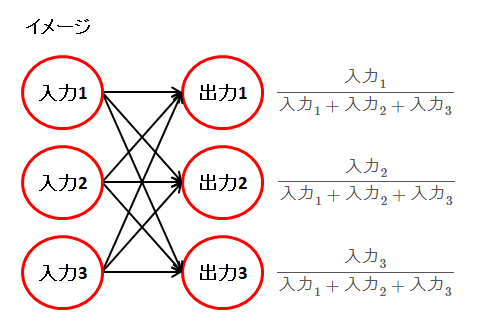
上記の入力値が 1、 2、3 だった場合、以下のようになります。合計すると 1 になります。

\( \dfrac{1}{1 + 2 + 3}\ \fallingdotseq 0.17 \)　　\( \dfrac{2}{1 + 2 + 3}\ \fallingdotseq 0.33 \)　　\( \dfrac{3}{1 + 2 + 3}\ = 0.5 \)


ソフトマックス関数の実装
import numpy as np

def softmax(lst):
    
    # リストの全要素に対して exp() を実行する
    exp_lst = np.exp(lst - np.max(lst))
    # RuntimeWarning: invalid value encountered in true_divide
    #exp_lst = np.exp(lst)
    
    # リストの全要素の合計を算出する
    exp_sum = np.sum(exp_lst)

    # リストの全要素を、上記の合計値で割る
    result_lst = exp_lst / exp_sum
    
    return result_lst


print(np.round(softmax([ 1,  10,   5]), 2)) # [0.   0.99 0.01]
print(np.round(softmax([-5, -10, -15]), 2)) # [0.99 0.01 0.  ]
print(np.round(softmax([15,  20,  10]), 2)) # [0.01 0.99 0.  ]
print(np.round(softmax([-5, -10,  10]), 2)) # [0.   0.   1.  ]

# 一番大きい値のインデックスの取得
print(np.argmax(softmax([10, 20, 30]))) # 2

Tag

New Article